plot3

가장 간단한 3차원 그래프는 “plot3” 함수이다. “plot3” 함수는 “plot” 함수와 거의 비슷한 방식으로 잘동하며 세 번째 입력 변수(보통 “z”)가 추가되어 있다. 다시 말해 2차원 공간에서 잇고자 하는 점들의 x, y 좌표를 서로 다른 벡터로 입력했던 것 처럼 3차원 공간에서 잇고자 하는 점들의 x, y, z 좌표 값들을 서로 다른 벡터로 만들어 입력하는 것이다. 가령 아래와 같이 3 차원 공간 상에 세 개의 점이 주어져 있고 이 점들을 선으로 연결시키고자 하는 경우에 “plot3”을 이용할 수 있다.

% (4, 5, 2), (2, 4, 3), (3, 2, 4)
x = [4, 2, 3];
y = [5, 4, 2];
z = [2, 3, 4];
plot3(x, y, z); 

이를 이용하면 아래와 같이 3차원 공간 상에 복잡한 그래프도 그릴 수 있다. 아래와 같은 예시를 우선 확인해보자.

t = linspace(0, 10 * pi, 1000);

x = exp(-t / 20).*cos(t);
y = exp(-t / 20).*sin(t);
z = t;
plot3(x, y, z, 'linewidth',2);
xlabel('x');
ylabel('y');
zlabel('z');
grid on;

위의 예시에서 볼 수 있듯이 “plot3”의 기본 문법은 아래와 같으며,

plot3(x, y, z, 'Name', 'Value')

대부분의 문법이 “plot”과 비슷하기 때문에 2차원 그래프 그리기 편의 “plot”에 대한 설명을 참고하거나 MathWorks 홈페이지의 공식 문서를 확인하자.

다만 3D 그래프를 다룰 때 2D와 다른 점 중 하나는 카메라 시점이라고 할 수 있는데 3차원 물체를 2차원에 표시하다보니 어떤 각도에서 바라보는 것 처럼 보여줄 것인가를 결정해야 하기 때문에 이런 추가 개념이 있다고 할 수 있다. 카메라 시점을 바꿔보기 위해서는 그래프를 드래그하거나 아래의 그림에서 보여주는 것 처럼 “Rotate 3D” 버튼을 누른 뒤 마우스로 드래그 할 수 있다.

카메라 시점을 바꾸기 위한 함수는 “view”이다. “view”의 기본 문법은 아래와 같은데,

view(az, el);

“az”와 “el”은 각각 azimuth(방위각), elevation(고도각)을 나타내는데 시각적으로는 아래와 같이 설명할 수 있다.

다시 말해 방위각을 키워주면 z 축을 중심으로 시계 반대 방향으로 회전하게 되고, 고도각을 90도까지 키워주면 정수리 방향에서 본 조감도를 보는 것과 같은 카메라 시점에서 3차원 그래프를 보게 되는 것이다.

아래는 다양한 시점에서 3차원 그래프를 확인한 예시이다.

t = linspace(0, 10 * pi, 1000);

x = exp(-t / 20).*cos(t);
y = exp(-t / 20).*sin(t);
z = t;

figure;
subplot(2,2,1); plot3(x, y, z, 'linewidth',2); grid on;
view(-37.5, 30); % view(3)와 동일
title('default camera position'); 
xlabel('x'); ylabel('y'); zlabel('z');

subplot(2,2,2); plot3(x, y, z, 'linewidth',2); grid on;
view(-10, 10); title('Az = -10, El = 10');
xlabel('x'); ylabel('y'); zlabel('z');

subplot(2,2,3); plot3(x, y, z, 'linewidth',2); grid on;
view(0, 90); % view(2)와 동일
title('Az = 0, El = 90');
xlabel('x'); ylabel('y'); zlabel('z');

subplot(2,2,4); plot3(x, y, z, 'linewidth',2); grid on;
view(90, 0); title('Az = 90, El = 0');
xlabel('x'); ylabel('y'); zlabel('z');

위 코드에 적힌 것과 같이 view(2) 혹은 view(3)이라고 입력해주면 조감도 시점 및 기본 시점을 바로 사용할 수 있다.

surf

3D 곡면 그래프를 그리기 위해서는 “surf”를 사용할 수 있다. “surf”는 “plot3”에 비해서 조금 사용하기 어려운 감이 있다. 아무래도 선을 쭉 연결해주는 것 보다는 면을 그리기 위해 필요한 부차적인(?) 세팅이 더 들어가기 때문이다.

일단 “곡면”의 방정식이 어떤 것인지부터 생각해보자. 가령 아래와 같은 방정식은 곡면의 방정식이라 할 수 있다.

우선 가장 간단하게 Geogebra 같은 사이트에서 이 곡면을 그려보면 아래와 같은 형태를 띈다는 것을 알 수 있다.

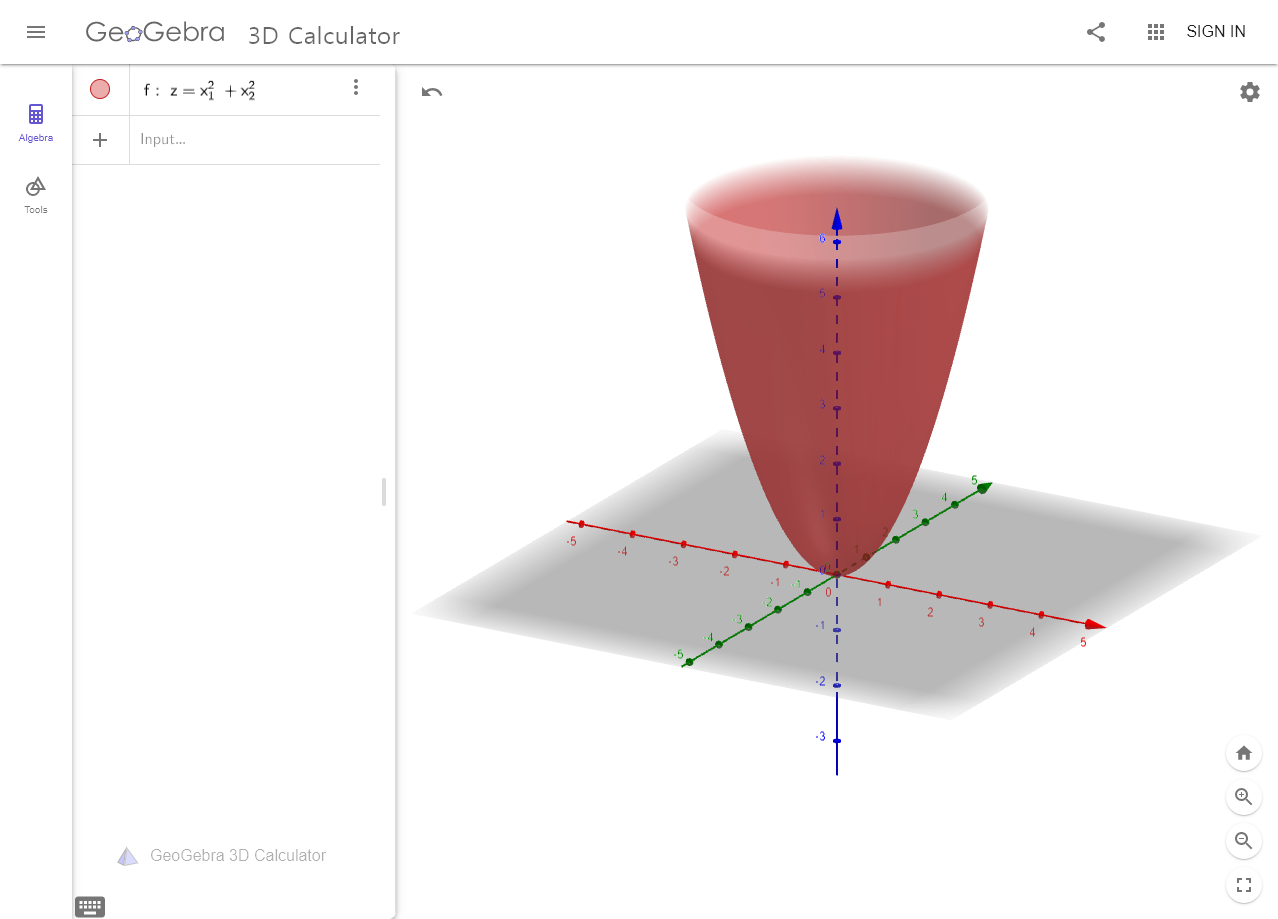
이 그림을 그리기 위해 “x”를 -2에서 2까지, “y”를 -2에서 2까지의 범위로 설정하고 “surf”함수를 이용해 그림을 그려낼 수 있는지 확인해보자.

x = -2:2; y = -2:2;
z = x.^2 + y.^2;
surf(x, y, z)

위 코드를 작동시켜 보면 아래와 같은 에러가 발생하면서 그림을 그릴 수 없다고 한다.

Error using surf
Z must be a matrix, not a scalar or vector.

에러 메시지에서는 “Z”에 해당하는 “z” 가 행렬이어야 한다라고 나온다. 근본적으로 이 방법이 잘못된 이유는 곡면에 대해 정의하기 위해선 “x”과 “y” 축 상의 값들만 정의해야 할 것이 아니라 xy 평면 상의 격자 점(grid points)들에 대해 함수값을 정의해야 하기 때문이다. 아래의 그림을 통해 x: -2, -1, 0, 1, 2, y: -2, -1, 0, 1, 2 값에 해당하는 격자점들이 어떻게 구성되어 있는지 확인해보자.

위 격자에 해당하는 x, y 값들을 행렬 형태로 각각 나열하면 아래와 같다. 이 때, 이미 눈치 챈 사람도 있겠지만 y 축의 방향이 우리가 보통 생각하는 y 축의 방향과 반대 방향이다. 이것은 수학적으로 xyz 축을 모두 표시할 때는 위 그림에 있는 것과 같이 오른손 법칙을 따라 xyz 축의 양의 방향을 정하기 때문이다.

x_new = [-2, -1, 0, 1, 2;
    -2, -1, 0, 1, 2;
    -2, -1, 0, 1, 2;
    -2, -1, 0, 1, 2;
    -2, -1, 0, 1, 2];

y_new = [-2, -2, -2, -2, -2;
    -1, -1, -1, -1, -1;
     0, 0, 0, 0, 0;
     1, 1, 1, 1, 1;
     2, 2, 2, 2, 2];

이제 이 격자 점들을 이용해 새롭게 “z_new”를 정의하고 “surf” 함수를 이용해 곡면을 그릴 수 있다.

z_new = x_new.^2 + y_new.^2;
surf(x_new, y_new, z_new)
xlabel('x-axis');
ylabel('y-axis');
zlabel('z-axis')

meshgrid

그런데 매번 곡면을 그릴 때 마다 위 설명에서와 같이 격자점의 값들을 생각해주기는 어려울 것이다. 이 과정을 수월하게 해주는 함수는 “meshgrid”라는 함수이다. 위 “x_new”, “y_new” 값을 쉽게 얻기 위해서는 아래와 같이 “meshgrid”함수를 이용할 수 있다.

[x_new, y_new] = meshgrid(-2:2);

따라서, 격자를 더 촘촘하게 해서 $z(x, y) =x^2 + y^2$ 그래프를 그리고 싶다면 이와 같이 수행할 수 있을 것이다.

[x, y] = meshgrid(-2:0.2:2);
z = x.^2 + y.^2;
surf(x, y, z);

주의: X, Y 축이 뒤집힌 것 처럼 보이는 현상

아래의 명령어를 이용해 얻은 “x”와 “y” 값을 직접 확인해보자.

[x, y] = meshgrid(-2:0.2:2);

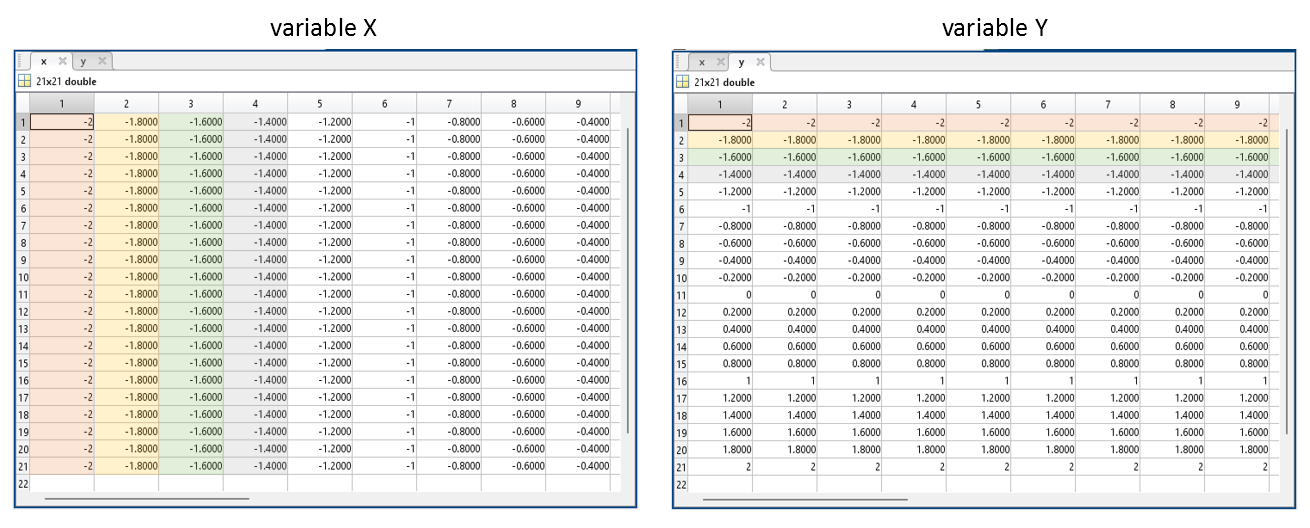
이 그림을 잘 보면 x 좌표와 y 좌표는 행과 열에 대응되지 않고, 거꾸로 x 좌표는 열에 대응되고 y 좌표는 행에 대응된다는 것을 알 수 있다. 이 결과는 지금까지 격자점을 정의하는 과정으로부터 차근히 검증해온 결과이므로 당연하다고 느낄 수도 있지만 가끔 이러한 결과는 분석 과정을 헷갈리게 할 때도 있다. 특히, 아래와 같이 “meshgrid”로부터 나온 격자점 좌표를 이용하지 않고 “for 루프”¹를 이용해 함수를 정의해서 사용하는 경우 결과물이 뒤집어져서 출력될 수 있다. 이런 경우 최종 결과물을 전치(transpose) 해서 곡면을 그리는 것도 방법이다.

x = -2:0.25:2;
y = x;
[X,Y] = meshgrid(x);
F1 = X.*exp(-X.^2-Y.^2);

F2 = zeros(size(X));
for i = 1:length(X)
    for j =1:length(Y)
        F2(i, j) = x(i) * exp(-x(i)^2 - y(j)^2);
    end
end

figure('position', [216, 422, 1082, 420], 'color', 'w');
subplot(1,2,1);
surf(X,Y,F1)
xlabel('x-axis'); ylabel('y-axis'); zlabel('z-axis');
title('Created with vector calculation')
subplot(1,2,2);
surf(X, Y, F2) % This should be surf(X, Y, F2');
xlabel('x-axis'); ylabel('y-axis'); zlabel('z-axis');
title('Created with for loop')

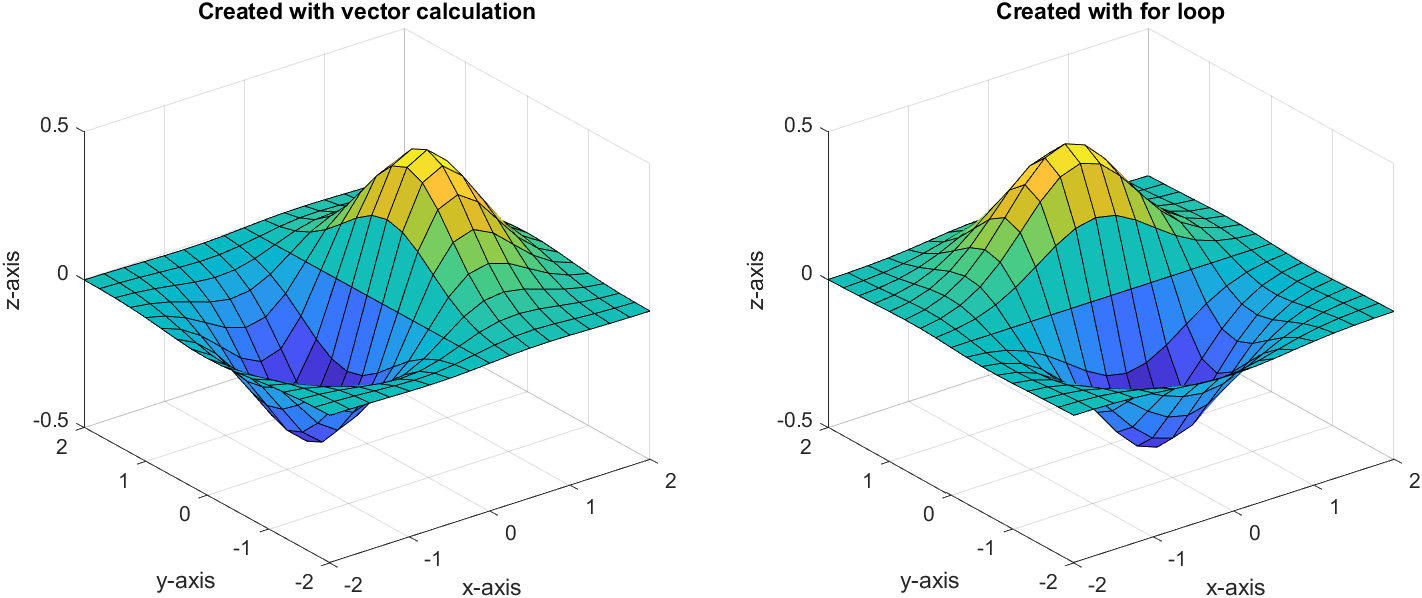
mesh

mesh 함수는 곡면을 그릴 때 면 없이 그물망(mesh)만 그리는 기능을 수행한다. 어떤 경우 mesh로 시각화 하는 것이 surf 보다 좋을 때도 있어서 이런 함수도 제공되는 것 같다.

x = -2:0.25:2;
y = x;
[X,Y] = meshgrid(x);
F1 = X.*exp(-X.^2-Y.^2);

figure;
mesh(X,Y,F1)
xlabel('x-axis'); ylabel('y-axis'); zlabel('z-axis');

contour

contour 함수는 등고선을 그려주는 함수이다. 어떨 때는 3차원 공간에 그림을 그리는 것 보다 곡면의 등고선을 그려주는게 함수의 형태를 쉽게 이해하게 해준다. 다시 말해, 어떤 방향이 가파른 방향인지 한눈에 파악하기에는 등고선이 더 시각적으로 도움이 될 수 있다.

x = -2:0.25:2;
y = x;
[X,Y] = meshgrid(x);
F1 = X.*exp(-X.^2-Y.^2);

figure;
contour(X,Y,F1)
xlabel('x-axis'); ylabel('y-axis'); 
grid on;

또, surf와 contour를 함께 이용하는 경우도 있는데 이 때는 contour의 객체를 이용해 등고선이 그려지는 z 축의 위치를 조정해야 한다. 그래픽스 객체에 관해서는 그래픽스 - 그래픽스 객체 다루기 편에서 자세하게 다루도록 하자.

x = -2:0.25:2;
y = x;
[X,Y] = meshgrid(x);
F1 = X.*exp(-X.^2-Y.^2);

figure;
surf(X, Y, F1);
hold on;
[~, h] = contour(X,Y,F1);
h.ZLocation = "zmin";
xlabel('x-axis'); ylabel('y-axis'); zlabel('z-axis')
grid on;

참고문헌

• Elementary 3-D Plotting (Plotting in Three Dimensions) (MATLAB)
• Do Matlabs 3D plots swap axes?